Blog.

Understanding Auto gradients

Cover Image for Understanding Auto gradients
Mayank Jain
Mayank Jain

Can you list down important algebra operations commonly needed for various machine learning algorithms specially neural networks ? Most common ones are simple matrix/tensor addition, subtraction, multiplication, division , Apart from that you also need exponential , tanh etc.

But one of the most important of these operations are derivatives, You may have heard of the term gradient if you have read about neural network training, For training any neural networks, There are two passes, First one is forward pass , where you perform a series of linear and non linear operations on input matrix to come up with output. And then for actual training of these neural networks you need to do backward pass, Where you need to calculate gradient of forward pass operations so that you can update your weights based on these gradients, For calculating these gradients you need the ability to do efficient differentiation of arbitrary function, Historically these differentiation operations are done manually by calculating equations of gradient of functions, but this manual calculation of differentiation is often error prone, with risk of bugs in your code and numerical accuracy , It also costs lots of manual effort and productivity loss. To solve this problem now most of the library support automatic gradient calculation, with newer libraries e.g. Autograd, Jax, PyTorch, TensorFlow 2.0 even giving very good easy to understand native python support of auto-gradients in their Ecosystem. Take a look at these code snippets to understand gradients better using Autograd and Pytorch.

Step 1 : Install and Import autograd in your python file or jupyter notebook

import autograd.numpy as np 
from autograd import grad

Step 2: Define function

# Define a function
def tanh(x):
    y = np.exp(-2.0 * x)
    return (1.0 - y) / (1.0 + y)

Step 3: Calculate Gradients

grad_tanh = grad(tanh)
print(grad_tanh(1.0))
print((tanh(1.0001) - tanh(0.9999)) / 0.0002)

Output:

0.419974341614026
0.41997434264973155

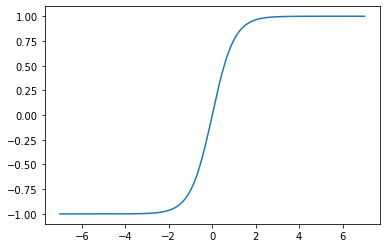
Step 4: Plot function over an interval:

import matplotlib.pyplot as plt
from autograd import elementwise_grad as egrad
x = np.linspace(-7, 7, 200)
plt.plot(x, tanh(x))
plt.show()

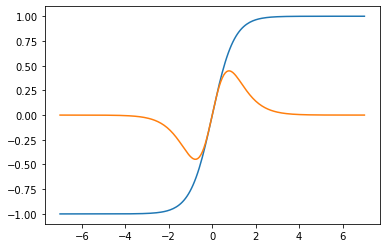
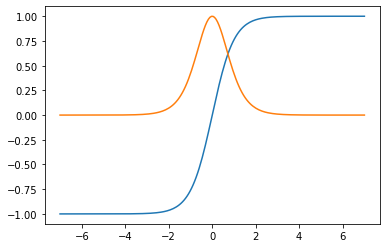
Output

Step 5: Plot gradient over interval: 

plt.plot(x, tanh(x), x, egrad(tanh)(x))
plt.show()

Output

Equivalent code in PyTorch: 

import torch
import numpy as np
import matplotlib.pyplot as plt
# Define a function
def tanh(x):
    y = torch.exp(-2.0 * x)
    return (1.0 - y) / (1.0 + y)

x = torch.tensor(1.0, requires_grad = True)
z = tanh(x)
z.backward() #Computes the gradient 
print(x.grad.data) #Prints '3' which is dz/dx 
print((tanh(torch.tensor(1.0001)) - tanh(torch.tensor(0.9999))) / 0.0002)

which Prints Results :

tensor(0.4200)
tensor(0.4202)

Plot function and gradient over interval: 

x = np.linspace(-7, 7, 200)
x = torch.from_numpy(x)
x.requires_grad_(True)
tan_h_of_x = tanh(x)
# Calculate Gradients 
tan_h_of_x.backward(x.clone())
# Plot function and Gradients over interval: 
plt.plot(x.detach().numpy(),tan_h_of_x.detach().numpy(),
         x.detach().numpy(), x.grad.data.detach().numpy())
plt.show()

Output